Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
Tags
- Python
- Kotlin In Action
- 20055 컨베이어 벨트 위의 로봇
- Kotlin in action 3장
- Kotlin in action 5장
- Kotlin
- 스프링 컨테이너와 스프링 빈
- KotlinInAction
- 객체 지향 설계와 스프링
- 컨베이어 벨트 위의 로봇 Python
- 자바 ORM 표준 JPA 프로그래밍 7장
- 싱글톤 컨테이너
- 20055
- 스프링 핵심 원리 이해
- 코틀린
- 코틸린인액션
- 백준
- 백준 13460 Python
- 스프링 핵심 원리 - 기본편
- spring
- 코틀린인액션
- Kotlin in action 10장
- kotlin in action 정리
- 고급매핑
- 백준 20055 컨베이어 벨트 위의 로봇
- 13460 구슬탈출 2
- Kotlin in action 6장
- 7장 고급매핑
- 스프링 핵심 원리
- 기능개발 python
Archives
- Today
- Total
기록하는 습관
[백준] 9934 완전 이진 트리 본문
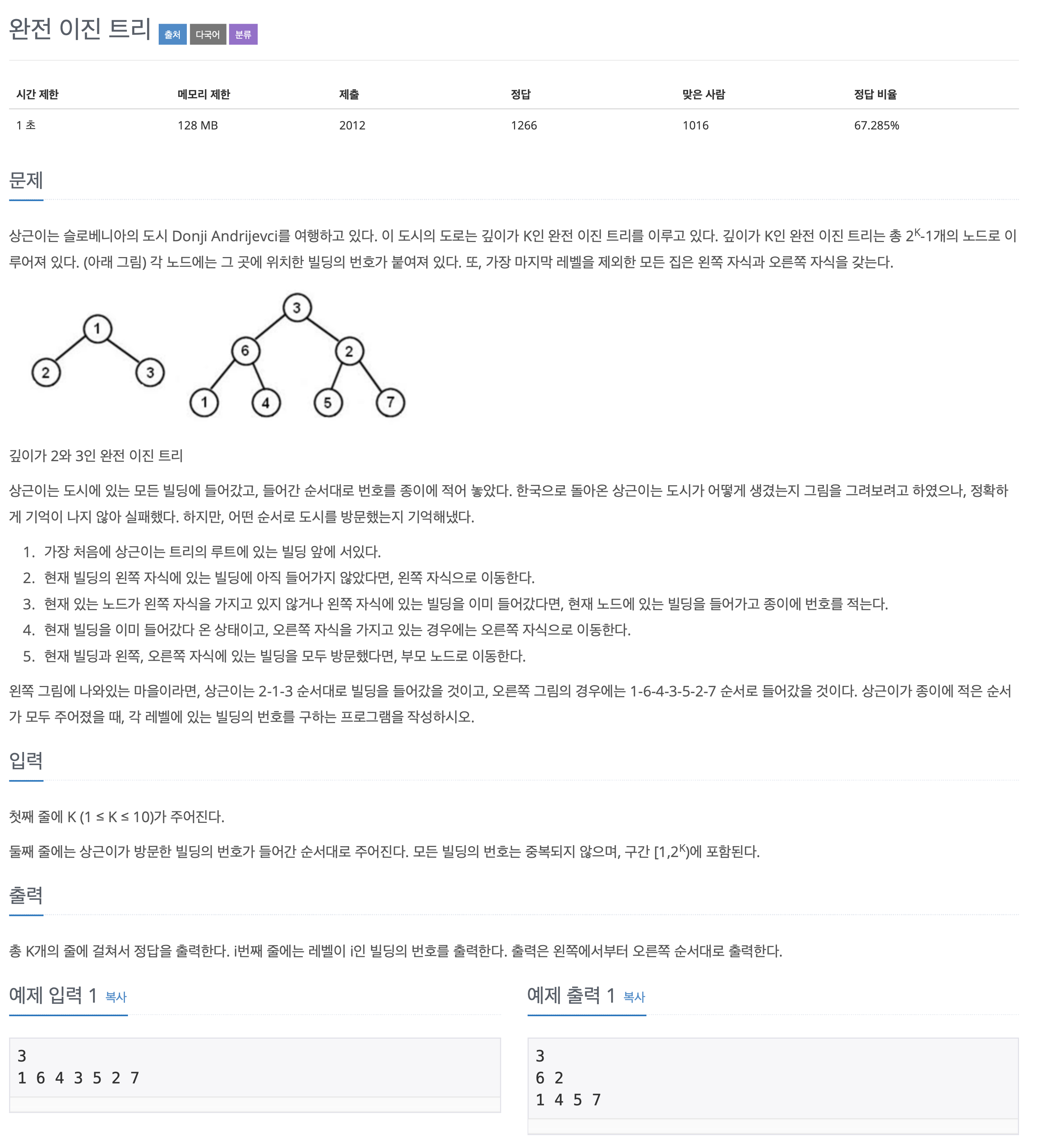
문제
코드
K = int(input()) # 입력 받는 K
building = list(map(int, input().split())) # 입력받는 배열
answer = [0] * (2 ** K + 1)
index = 0 # 입력 받은 배열 building을 순회할 때 사용하는 index
def inorder(i, depth): # 중위 순회
global index
if depth == K: # base condition
answer[i] = building[index]
index += 1
else:
inorder(i * 2, depth + 1)
answer[i] = building[index]
index += 1
inorder(i * 2 + 1, depth + 1)
inorder(1,1)
count = 1 # answer[1] 부터 출력
for i in range(K):
for j in range(2**i):
print(answer[count], end=' ')
count += 1
print()
풀이
- 첫 번째 생각: 트리를 만든 후, 값을 차례대로 넣어주고 level마다 출력하기 -> 노드를 초기화 해주는 작업이 추가로 필요하다.
- 두 번째 생각: 완전 이진 트리 특성을 이용하여 트리 만들지 않고 배열로 해결하기
두 번째 생각
- 완전 이진 트리 특성: 부모 node를 기준으로 left node는 부모 노드 index * 2, right node는 부모 노드 index * 2 + 1이 된다.
- 위 문제는 중위 순회인 것을 파악하고 중위 순회를 한다.
- 중위 순회: left node -> parent node -> right node
- 앞서 얘기한 완전 이진 트리 특성 + 중위 순회 개념을 합쳐서 아래 코드 작성.
-
inorder(i * 2, depth + 1) answer[i] = building[index] index += 1 inorder(i * 2 + 1, depth + 1)
- base condition은 depth가 K일 때로 하고 answer = building[index] 해준다.
개념
완전 이진 트리: 이진 트리 중 노드가 왼쪽 부터 차례대로 채워져 있는 트리
포화 이진 트리: 이진 트리 중 자식 노드 2개가 모두 채워져 있는 트리
아래 그림은 포화 이진 트리이면서 완전 이진 트리이다.

완전 이진 트리 특성
- root 노드 index를 1이라고 한다면, left node는 index * 2, right node는 index * 2 + 1이 된다.
전위 순회 (pre-order traversal)
루트 노드 -> 왼쪽 노드 -> 오른쪽 노드 순으로 방문한다.
후위 순회 (post-order traversal)
왼쪽 노드 -> 오른쪽 노드 -> 루트 노드 순으로 방문한다.
중위 순회 (in-order traversal)
왼쪽 노드 -> 루트 노드 -> 오른쪽 노드 순으로 방문한다.
'알고리즘 > [문제풀이] 백준' 카테고리의 다른 글
| [백준] 2178 미로 탐색 (Python, BFS) (0) | 2021.06.06 |
|---|---|
| [백준] 1068 트리 (0) | 2021.06.02 |
| [백준] 14425 문자열 집합 (0) | 2021.05.23 |
| [백준] 11279 최대 힙 (0) | 2021.05.23 |
| [백준] 2504 괄호의 값 (0) | 2021.05.13 |
Comments




